# 赫夫曼树
赫夫曼树也叫做最优二叉树。
# 名词解释
由2,3,5,6,8构成的最优二叉树,如下图:
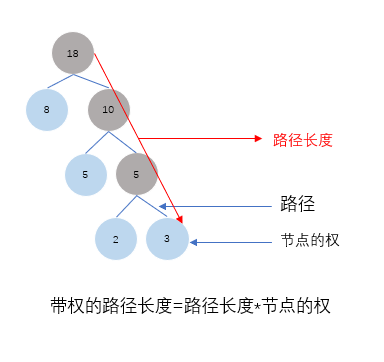
节点的权: 叶子节点的值
路径: 叶子结点与父节点的距离为1
路径长度: 指根节点到叶子节点的长度
带权的路径长度: 路径长度*节点的权
最优二叉树: 树的带权路径长度为树中所有叶子结点的带权路径长度之和最小。
# 原理
- 首先要求集合有序
- 取集合的两个最小值作为叶子节点,相加后得到的值插入有序集合,并删除原来的两个值
- 重复2步骤,直到集合只剩一下一个根元素即成为一颗二叉树,这就是最优二叉树
# 最优N叉树
# 原理
- 首先要求集合有序
- 取最小的n个节点作为叶子节点,相加后得到的值插入有序集合,并删除原来的n个值
- 重复2步骤,直到集合只剩下一个根元素即成为一颗n叉树,前3步同最优二叉树的步骤一样
- 遍历节点判断是不是标准的n叉树(有孙子节点的节点必须有n个子)
- 取孙子节点的最大节点补充该节点
- 重复4,5步骤,直到所有有孙子节点的节点都有n个子节点,即完整的n叉树,也是最优n叉树
# 原理图
构建一颗三叉树,重复步骤1,2,3
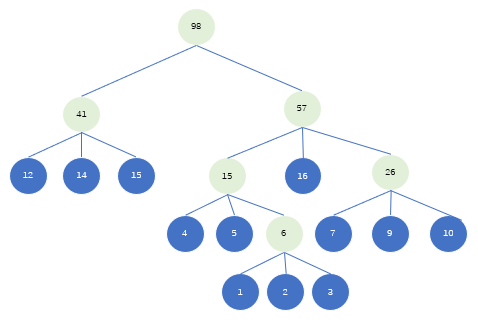
取孙子节点补齐98的子节点个数
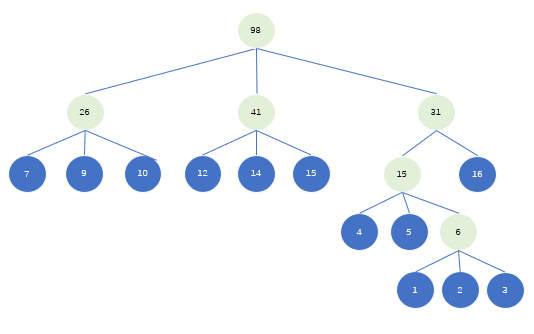
补齐节点31的子节点
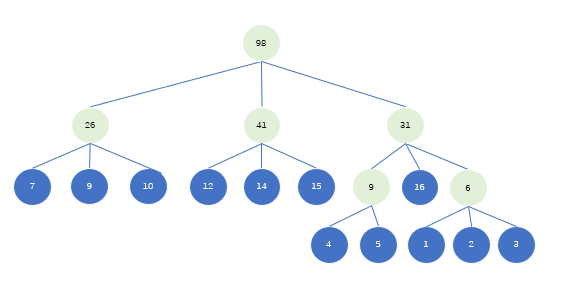
排序98的子节点,因为3个子都是节点类型,所以只排孙子节点就行了
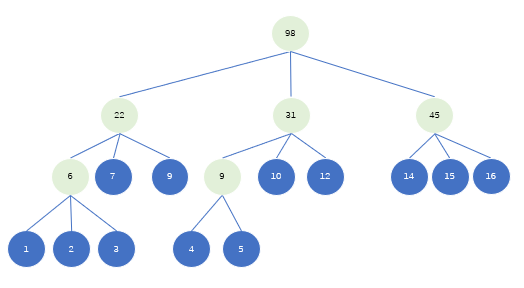
重复步骤4,5,直到所有的节点都是有序的三叉树,最后即得最优三叉树。
